龙形曲线的递归生成(dragon curve)

这是一道来自亚琛工业大学的题(RWTH Aachen University),讲到递归概念时的作业是用Java生成龙形曲线.既然做了,记录一下吧.

私认为Wiki英文版已经说的很全面了,值得参考:Dragon-curve(Wiki)

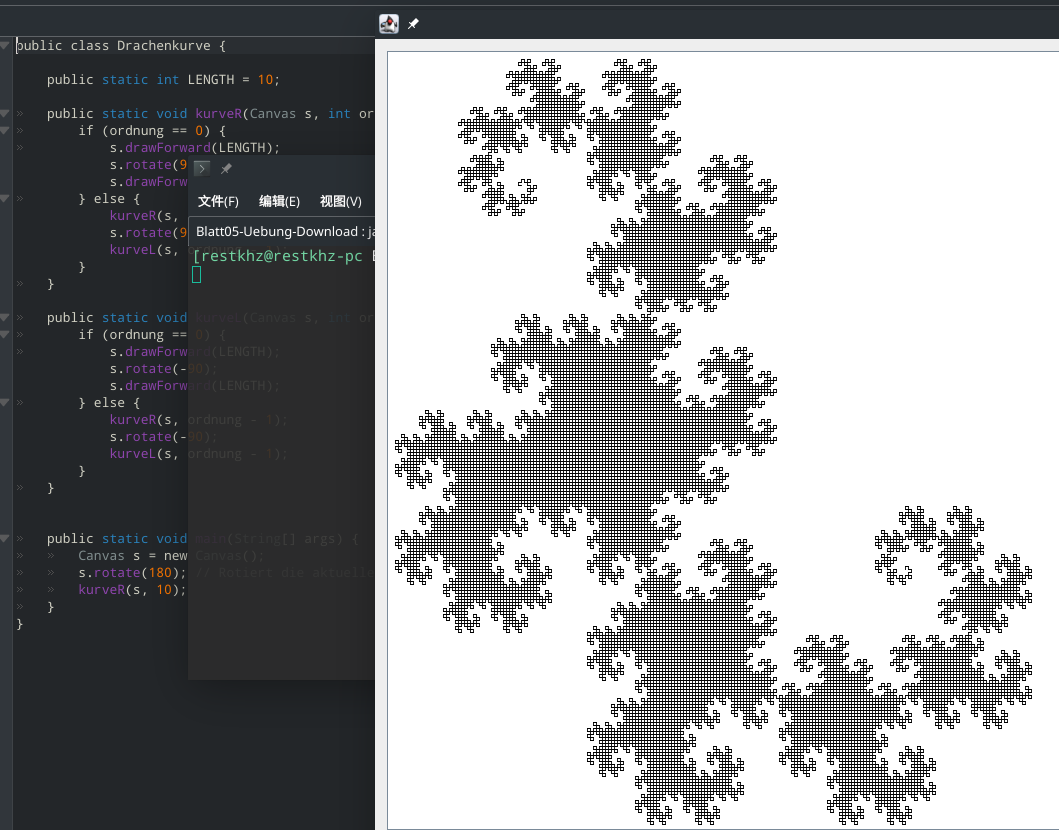
亚琛理工提供了绘图的Canvas代码,我们只需要调用drawForward画线,rotate旋转.

在弄清楚”这是什么”以后,如何转弯就成了重点,我们不难发现:
(R为右转90度,L为左转90度)

1. R
2. R R L
3. R R L R R L L

是在上一次迭代结果上,在每个元素两侧又添加了一对RL.
如何用递归实现呢?我在草稿纸上画了画.
我不太方便把草稿纸发出来,但是你可以根据这个特性自己手画一个满二叉树,每一层深度就是递归深度(你真的现在就要画一个,认真的),大概是:
R
R L
R L R L
这个样子.然后把这棵树”压扁”(父节点在子节点中间),后你会得到RRLRRLL
(有没有发现这其实是二叉树的中序遍历?)

好的,有思路了.我们已经解决了最关键的问题:如何旋转,
现在考虑在什么时候画线.

如果你在草稿纸上画了那个图,写了那一串RRLRRLL什么的,和树对应起来,你会发现,每一个叶节点(没有子节点的节点,最下面那一层)和其”前辈”节点是交错的.那么我们可以让叶节点画线,而其它节点只负责角度旋转.

于是我的代码就出来了.

public class Drachenkurve {

    public static int LENGTH = 10;

    public static void kurveR(Canvas s, int ordnung) {
        if (ordnung == 0) {
            s.drawForward(LENGTH);
            s.rotate(90);
            s.drawForward(LENGTH);
        } else {
            kurveR(s, ordnung - 1);
            s.rotate(90);
            kurveL(s, ordnung - 1);
        }
    }

    public static void kurveL(Canvas s, int ordnung) {
        if (ordnung == 0) {
            s.drawForward(LENGTH);
            s.rotate(-90);
            s.drawForward(LENGTH);
        } else {
            kurveR(s, ordnung - 1);
            s.rotate(-90);
            kurveL(s, ordnung - 1);
        }
    }


    public static void main(String[] args) {
        Canvas s = new Canvas();
        s.rotate(180); // Rotiert die aktuelle Ausrichtung nach oben
        kurveR(s, 10);
    }
}

Ordnung是这里的深度计数器
drawForward是画线,rotate是旋转,这两个函数来自大学提供的Canvas,毕竟大学的,我就不放出来了.