简单密码：写给程序员的密码学入门（三：古典密码，从凯撒到OTP）

讲到加密，就不得不想想它的历史故事。加密其实没有那么简单。

从凯撒位移说起

这个恐怕是最有名的古典密码了。怕观众不记得，给各位复习一下：
其实就是把整个字母都往右边移动了几位，至于几位这个就是密钥。很明显26个字母你只有25种移动方法，还有一个就是原来的样子。
比如下面这就移动了6位。

明文字母：ABCDEFGHIJKLMNOPQRSTUVWXYZ
密文字母：GHIJKLMNOPQRSTUVWXYZABCDEF

比如我想加密“BOB”那么就找对应的就行，B对应H，O对应U，结果是“HUH”.

它的缺点在哪里？很明显：

总共也就25个不同密钥，每个都试一试，结果肯定能出来啊。
统计学。根据字母出现频率，比如 E 在英文中出现频率极其高，那么我们只要分析哪个字母出现频率最高，它很有可能就是 E 。只要有足够的密文就会让统计更加准确，就有可能破解。

这个网站就可以做频率分析：http://quipqiup.com/

当然以上还是我们在只有密文的情况下,我们已经可以对密码分析。

实际情况，可能攻击者已经知道了更多…

比如一部分密文对应的明文，甚至可以接触到加密或解密的机器（程序）：
比如黑客已经知道“HELLO”加密后是“NKRRU”，那么可以很轻松的推断出位移（密钥）
如果黑客能接触到密码机呢…黑客输入“AAAA”出来了一个“DDDD”这不一眼就看出来密钥了嘛？

这里就引入根据攻击者知道的信息由少到多，对攻击的分类：

唯密文攻击：攻击者仅知道密文
已知明文：攻击者知道了部分密文相对应的明文
选择明文攻击：攻击者可以随意使用密码机生成密文，试图分析
选择密文攻击：攻击者可以随意用解密机解密密文，试图分析

所以加密算法必须抗住选择明文和选择密文才算行。
如果都拿到密码机还分析不出来，那么就更不可能已知明文，或者仅仅根据密文就能破解。

而凯撒位移甚至连唯密文都抗不住。呃…只能说是娱乐水平的了。千万别用！

Enigma机

其实简单的理解这玩意儿，就是：每次输入都会换偏移量的凯撒位移机器。

这玩意儿在当时给盟军破解造成了很多困难。但是在早期，波兰人找到办法通过已知德军明文中的重复规律（已知明文）大大降低了暴力的复杂程度。
而后德国人也不傻，随着开战，直接加俩转子，可能性翻几倍后，把波兰人整不会了。波兰在被拿下之前把这个技术给了英国。英国又发现，一个字母不可能在加密后变成它自己的特性，而恰好德语一个词又很长，所以能大概猜出这个词的位置。这又降低了可能性。

注意安全！！！

我在第一篇文章讲过，不要搞自己的加密算法。
绝大多数人发明的密码不会比Enigma更好。

我来举一个反例：

bad example

这里他用This is my coat.经过他的算法得出jZubpd!zn!tj!tiU
思考题：你能猜出他是怎么加密的吗?(提示：观察感叹号，还有周边字符数量)
这是已知明文了。
如果你猜出来一大半（因为这里信息未必够）那你就已经超越他认为的顶尖黑客了。
但是对于他开发的别的web项目，由于你能接触他加密脚本，那就是选择明文。只会更加不安全。

异或和OTP

你或许听过异或(XOR) 符号： $\oplus$ 是一个特别安全的加密…

从异或开始说起

给各位复习一下，我们先看看xor这个逻辑吧

xor	0	1
0	0	1
1	1	0

输入都是0或者都是1的时候，输出就是0. 但是输入一个0和一个1的时候，输出为1.

啊那为什么xor特别安全呢？

你会发现这个逻辑输出0和1的概率是均等的。也就是说，只要我们密钥概率足够随机，那出来的结果0和1也是随机各占一半。这样密文对于统计，统计不出什么啊。由于密钥随机，完全消灭了明文的特征，使得密文就像随机数，仅有密文的话目前认为不可破解。

而加密的过程也非常简单：明文 xor 密钥 = 密文
解密： 由于相同的东西经过xor会抵消，(密文) xor 密钥 = (明文 xor 密钥) xor 密钥 = 明文

这么好？那为什么我们不这样用xor加密？

别急，因为有缺陷，我们过一会讲
此外，其实有用，这就是OTP了

OTP（一次性密码本）

因为这玩意儿有xor的安全性，这是当年华盛顿-莫斯科电话专线的加密方式。也算是古典密码的高级玩意儿了。

那它是怎么做的呢？

密钥：你需要一个至少有明文长度那么长的随机并且一次性的密钥
异或：一位一位地让密钥和明文xor

就这么简单！

比如我们想加密“HALO”
先转换成二进制：H(01001000) A(01000001) L(01001100) O(01001111)

明文：01001000 01000001 01001100 01001111
密码：11011001 00100010 00101011 11111010 
---------------------------------------------------------------------
密文：10010001 01100011 01100111 10110101

单纯的OTP现在不常见了。我之前说它的缺陷：

你很难找到一个足够长并且足够随机的一次性密钥

长：如果你要加密1G的数据，那么你的密钥也必须有1G。啊，这还怎么玩？这1G的密钥你打算怎么给对方？

随机：随机其实很难。比如你有0到50这个区间的真随机数，现在你想把它乘二扩展成0到100区间，可以吗？

不可以。不然你得到的都是偶数。其实并不随机。

很多时候我们都是在用伪随机的。不信你开个python，用一样的随机数种子，你会发现出来的随机数是一样的。还有很多时候，很多人用时间戳当种子。如果我知道这个密钥是什么时候生成的，那么我也可以得到和你一样的密钥。

用操作系统的随机数发生器会好一些，比如/dev/random和/dev/urandom。前者质量好但是会不够用。后者质量略差但是够用。

一次性：xor的密钥必须一次性。如果有重复的话，带上已知明文，是可以获取到密码的。如果就算没有明文，我们依旧可以得到点什么。

前文说过，由于相同的东西经过xor会抵消
明文 xor 密文= 明文 xor (明文 xor 密钥 ) 这里明文抵消，直接得到密钥。

那么密钥因为重复而相同，但是不知道任何明文会怎么样呢？
密文1 xor 密文2 = (明文1 xor 密钥) xor （密钥 xor 明文2）= 明文1 xor 明文2
这里密钥会抵消，留下两个不同明文的xor。这有什么用？看图：

(图片来自： https://www.crypto101.io/ 的pdf的一段。这书很好。)

OTP留下了什么?

人们一直在想方设法改进OTP的缺点。因为他优点实在是…太香了。
那么它的缺点可以解决吗？
比如，我们可不可以根据什么方式生成足够长，足够随机的密码…

现代密码的流密码（stream cipher）就是这种思路。就像溪流一样，密码和明文源源不断地流进去，密文流出来。而流密码的重点就在：我们如何生成OTP的密码。

比如：通常人们用AES作为块加密，但是谁说AES不能作为流加密？

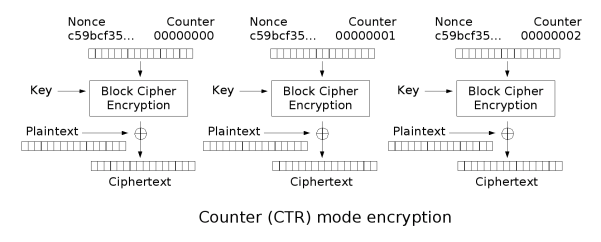
这是AES-CTR，你会发现这里的AES只是用key去加密随机的 Nonce和计数器(Counter)，AES产生的密文将作为一个类似随机数的东西，去和明文(Plaintext)异或得到真的密文(Ciphertext)

注意： $\oplus$ 是xor

(图片来自：wiki 公有领域)

而到了这里就已经逐渐步入现代密码学了。

简单密码：写给程序员的密码学入门（三：古典密码，从凯撒到OTP）