图论:从无向图到有向图基础笔记

前言

• 该笔记是以德国图论的一个贯穿PPT作为骨架,使用汉语/英语作为补充资料填充血肉最后整理成为汉语的终极缝合怪.
• 图片从外部wiki链入,不确保地球上所有能看到本文的人都能看到图.如果有必要,适当使用某些工具,刷新本页面后查看.已经把图上传到github.
• 因为是个人笔记,不确保准确.
• 内容来说仅仅是贯穿的概念梳理,不涉及算法和深入的推论.,如果你想深入学习推论证明和算法,时间宝贵,CTRL+F查找一下,没有的话现在可以离开了.
• 由于这个板块内容来自于不同教材,不同语言,不同标准之间翻译用词有点混乱. 我已经努力尝试规范用词问题,但是我很清楚,不一定正确妥当.
• 很多定义是我从英语和德语自己翻译过来的(非机翻),由于定义存在大量从句,奇怪的思维,可能写出的汉语会很奇怪.
• 如果发现错误,非常欢迎留言,帮助我学习.在此先感谢!

无向图(Ungerichtete Graphen [engl. Undirected graph])

定义

无向图G可以用一个二元组(Paar)表示.$G=(V,E)$,在此处V是一个由顶点(德:Knoten英:vertices)组成的有穷,非空集合. 集合E是 集合V的 双元素子集的 集合的 子集 .( Die Menge E ist eine Teilmenge der Menge der zweielementigen Teilmengen von die Menge V ,我看到这句绕口令的时候也是想掀桌子的 :) )写做:

$E \subseteq { {x,y } | x,y \in V, x \neq y }$

E中元素叫做边(德:Kanten英:Edges)

简单说,就是一个二元组,每个元都是一个集合,记录了点和他们之间的连接状态.

实例

The diagram is a schematic representation of the graph with vertices $V={1,2,3,4,5,6} E={{1,2},{1,5},{2,3},{2,5},{3,4},{4,5},{4,6}}$

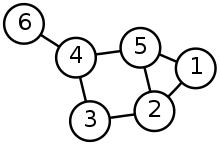
(来源https://en.wikipedia.org/wiki/Graph_(discrete_mathematics)))

一些特殊的无向图图

完全图(Vollständiger Graph [engl. Complete graph])

写作$K_n$.n是顶点数量. 每两个顶点之间都有边连接.故其有$\frac{n(n-1)}{2}$条边.

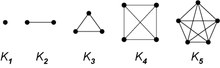
循环图(Kreisgraph [engl. Cycle graph])

(也有叫做环形图,环图,圈图,周期图的)
循环图写作$C_n$,n为顶点数量.由至少三个顶点组成,构成一个环形的图.

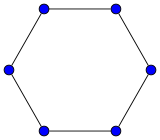
$V={v{1},\ldots ,v{n}}$

$E={{v{1},v{2}},{v{2},v{3}},\ldots ,{v{{n-1}},v{n}},{v{n},v{1}}}$

这个图属性很多, 目前先写这三点属性

• 每个定点度数均为2
• 顶点和边数量上相同.
• 连通图,欧拉图,哈密顿图(不懂先跳过)

链 (Pfad [engl. Chain/Path Graph])

链写作$P_n$, 恰好构成一条简单路径.呈链状. 可以认为是一个圈图去掉一个边使其收尾不相连.

超方体(Hyperwürfel)

方格图(Gittergraph)

邻域和度(Nachbarschaft und Knotengrad[engl. Neighborhood and degree])

对于图G=(V,E)的一个点v我们如此定义邻域$\Gamma(v)$:

$\Gamma(v):={ u \in V | { u,v} \in E }$

而对于度,如此定义:

$deg(v) := |\Gamma (v)|$

• 而对于任意的图,所有点的度数之合是边的两倍:$\sum _{v\in V}\deg(v)=2|E|$
• 奇数度数的顶点的数量为偶数,握手定理

对于这张图:

• $\Gamma(1) = { 5,2}$
• $deg(v) = 2$
• $\Gamma(4) = { 3,5,6}$$
• $deg(4) = 3$

一些定义

端点 (Endknoten [engl. End-vertex])

对于一个边$e={ u,v} \in E$,u和v被成为e的端点.(对于有向图同样适用,只不过根据方向两个端点被分为起点和终点)

相邻(Adjazent [engl. Adjacent])

两个顶点${u,v} \in E$ 被称为相邻.即两个被一条边连接起来的顶点,他们之间的关系是相邻的.

关联(Inzident [engl. Incident])

如果v是边e的一个端点,那么这个顶点和边的关系叫做关联.

注意!相邻是两个点的关系,而关联是点和边的关系!

通路及相关定义

这里是图论命名和翻译混乱的地方.尤其是我还要理清三种语言里的概念,可能读起来令人头晕.

通路/途径 (Wege [engl. Path/Walk])

.

在德国教材中定义:通路是一个长度为$l. l \in \mathbb{N}$的序列,表示为$W = (v0,v_1,…v_l),v\in V$的序列.(${ v_i,v{i+1} } \in E, i =0,\dots,l-1$)

其中v0是起点(Anfangsknoten),vl是终点(Endknoten).

Pfad

这个概念我不知道如何翻译

指一个Weg(通路/途径),其中所有顶点均不同.

(相比于中文/英文资料均不同. 不是中文路径/通路(Path),在此处不允许出现回路)

Kreise

这里和中文的圈或者环,也不是circuit或者cycle,略有出入

指一个序列,长度为l且l大于等于3,首尾相邻,且边不重复,注意,有向图的Kreise是不需要有长度限制的

写做$C=(v1, \dots , v_l),\quad { v_1, v_l} \in E \quad and \quad { v_i, v{i+1}} \in E, for all \quad i=1,\dots l-1$

对,这里的序列首尾根本不是同一个点

这些三个语言的定义都不太一样. 地理隔离导致生殖隔离了?

文献混乱的定义整理

在GRAPH THEORY WITH APPLICATIONS( J.A Bondy and U.S.R. Murty )中的定义如下:

A walk in G is a finite non-null sequence W = v0 e1 v1 e2 v2… ek vk, whose terms are alternately vertices and edges,

If the edges e1,e2,….,ek of a walk W are distinct, W is called a trail.

In addition. the vertices v0,v1,…,vk are distinct, W is called a path.

在 《离散数学及其应用》中通路(Path)在图并非简单图时使用点边交错序列, 在简单图中使用纯顶点序列(因为简单图两点之间边唯一)

若通路(Path)起点终点在相同顶点上,并且长度大于0,那么称为回路(circuit)

如果回路没有重复顶点和边那么称为简单(simple)这样的路径为简单路径(simple path)这样的回路称为简单回路(simple circuit),(我自己注明,这个简单回路概念有些地方还叫做环或者是圈这类的东西)

子图 (Teilgraph [engl. subgraph])

德语中名字很多:Teilgraph oder Untergraph oder Subgraph

设存在图$H=(V_H,E_H),G=(V_G,E_G)$

当$V_H\subseteq V_G$ 并且 $E_H \subseteq E_G$

那么H就是G的子图

导出子图/诱导子图 ( induzierten Teilgraphen [engl. Induced subgraph])

接着子图的定义,如果:

$E_H = E_G \cap { { v_1,v_2} | v_1 \in V_H, v2 \in V_H }$

便是诱导子图. 这个定义看着有点迷糊,诱导子图就是:一个子图,它剩下的那些点之间的边,如果原图有,那么它也要有.

连通图(Zusammenhängende Graphen [engl. Connected graph])

指对于任意两个不同顶点,都存在通路的图

$G=(V,E)\quad u,v \in V,u \neq v$

连通分量(Zusammenhangskomponente [engl. connected component])

在无向图中G的子图H,在:

1. H是连通的
2. G没有别的连通的子图连通且包含H

时被称为连通分量.

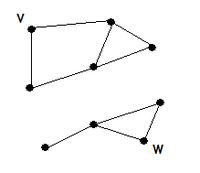
这是wiki的图,能看出来这张非连通图的V和W两点不通. 有两个连通分量.

这两个连通分量就是上面一大块和下面一大块,首先,他们之中的每个点是连通的,其次,他们是最大的子图.

所以连通图的连通分量是它自身

一些相关定理

1. 一张图G=(V,E)至少有 |V|-|E|个连通分量.
2. 对于每个连通图G=(V,E)都有$|E|\ge |V|-1$

多重图(Multigraphen [engl. Multigraph])

(也有称为伪图pseudograph)

就是有多重边的图(两个顶点之间边不唯一),有时候也会在边上加一个数字表示.

如下图,来源于柯尼斯堡问题.

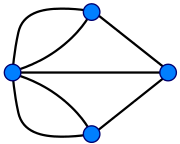
柯尼斯堡七桥问题,欧拉通路和欧拉回路(Eulerwege und Eulerkreise)

这个问题不得不提那个柯尼斯堡七桥(现在是加里宁格勒)问题

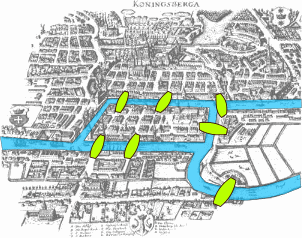
如图,简而言之,如何每个桥只走一遍,走完所有的桥?

欧拉通路(Eulerwege)

引申自柯尼斯堡七桥问题,欧拉通路是一种

1. 边不重复的通路(个人觉得类似于GRAPH THEORY WITH APPLICATIONS( J.A Bondy and U.S.R. Murty )中的trail概念)
2. 遍历了图中所有边

欧拉回路(Eulerkreise)

类似于欧拉通路,欧拉回路:

1. 一个kreise
2. 包含图中所有边

两者区别

其实就是有没有回到原点.在有些图里,存在欧拉通路,但是不存在欧拉回路.在 离散数学及其应用 中出现过例子

回到柯尼斯堡

经过欧拉通路和欧拉回路的定义,那么柯尼斯堡七桥问题就是:是否存在欧拉通路?

• 欧拉回路充要条件:如果G=(V,E)是一个连通图, 如果要存在欧拉回路,那么所有的顶点度数必为偶数.(因为每次遍历到这个点的时候,入度+1,出度+1,遍历一次总共+2所以必为偶数)
• 欧拉通路充要条件:如果G=(V,E)是一个连通图, 除了欧拉回路存在情况以外(所有顶点度数为偶数),也可以有两个顶点度数为奇数(奇数两个点分别是起点和终点.因为奇数顶点作为起点比别的顶点多了一个出度,终点比别的顶点多一个入度.所以deg+1,在正常遍历点数+2的情况下偶数加奇数,结果必为奇数.)

哈密顿通路和哈密顿回路(Hamiltonwege und Hamiltonkreise)

来自哈密顿问题

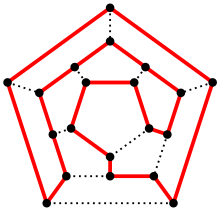
和欧拉通路和欧拉回路相似,
只不过哈密顿通/回路是遍历所有点且不重复.

然而这个问题目前是NPC问题,所以目前还没有像欧拉通/回路一样简单的判断方法.

和超方体联系

任何一个层数大于等于3的超方体都存在一个哈密顿回路.

有向图(Gerichtete Graphen [engl. Directed graph])

(Digraph)

在我先在用的教材里,有向图使用一个二元组D表示.D=(V,A),此处V是一个表示所有顶点的非空集合.集合A:$A \subseteq V \times V$用二元组表示有向的边(engl. Arcs)

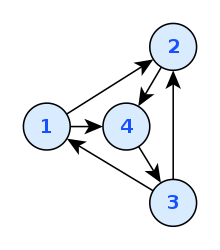
如图,比如(3,2)就是一条边.

入度和出度(Eingagsgrad und Ausgangsgrad)

一个顶点,有几个指向它的边就有一个入度,指出多少个边就有多少出度.

• 入度 $indeg(v) := | { u \in V| (u,v) \in A} |$
• 出度 $outdeg(v):= | { u \in V | (v,u) \in A } |$

所以对于每个有向图入度等于出度

$\sum{v \in V} indeg(v) = \sum{v \in V} outdeg(v)$

而indeg(v)+outdeg(v)也被称为v的度数(Grad [engl. degree])

自环(Schleifen [engl. loop])

假设上图中如果有(3,3)这样自己指向自己的边,那么这个叫做自环.(好像没有在无向图提到)

有向无环图: DAG (Kreisfreie Graphen [engl. directed acyclic graph])

这里的Kreis和之前定义不同之处在于,长度不必大于等于3.也就是说,两个元素互相指着对方也是一个Kreis.我们称之为环

比如一个图a,b互相指向对方,那么(a,b)(b,a)都是环.

而DAG就是指没有环的图.

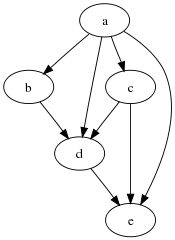
拓扑排序(Topologische Sortierung [engl. topological ordering])

拓扑逻辑是一个带有|V| = n的有向图D=(V,A)的双射函数s:V→{1,….,n}

对于所有边$(u,v) \in A , s(u)<s(v)$

当一个有向图没有环的时候必有拓扑排序.所以,有且仅有DAGs存在拓扑排序.

拓扑排序可以描述一个线性任务顺序. 每个任务(顶点)指会出现一次,如果A在B之前,那么不存在B到A的路径.

画图的时候可以找出没有入度,出度多的点放在最前面开始,没有出度的放在最后. 有一些算法解决这个问题但是这里就不说了.

德语Wiki的解释很有趣,比英文的好玩.这是一次起床穿衣的拓扑排序.无论如何,内裤得先穿上,再穿裤子.咱不是超人,对吧.

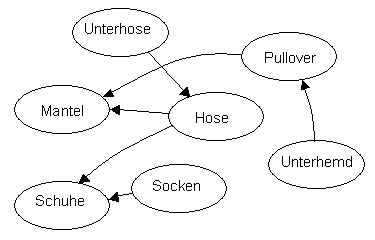
基图(Zugrunde liegender Graph)

每个有向图都可以转换成一个无向图:

• 每个边(u,v),u不等于v,转换为无向的{u,v}
• 删除掉自环
• 把多重边替换成为单边

此时的无向图就是原本有向图的基图 zugrunde liegende ungerichtete Graph.

有向图的连通(Zusammenhängende gerichtete Graphen)

强连通 (stark zusammenhängend)

当D=(V,A)中每一对不同的顶点之间都存在Pfad,那么便称为强连通.

弱连通 (schwachzusammenhängend)

如果有向图D的基图G是连通图,那么D就是弱连通图.

树的图论笔记在这里,可以继续阅读:图论:形形色色的树和森林