图论:形形色色的树和森林

前言

• 这部分整理了图论中的树,森林,匹配,着色,二叉树之类的基本概念.其实应该和上一笔记是整体.
• 如果遇到看不懂的部分,请阅读图论:从无向图到有向图基础笔记
• 其它前言废话也见上一篇笔记.

树和森林 (Bäume und Wälder)

树和森林的一些定义

树是一个连通的,无环的图. 一个森林是存在连通分量的图,其连通分量是树.

我们把树写为: T=(V,E)

而一个树中的带有度数为1的节点v被成为叶(Blatt),而一个|V|>=2的树图去掉叶节点依旧是树.

• 每个带有|V|>=2的树T=(V,E)至少存在两个叶节点.
• 树 T=(V,E) 存在 |E| = |V| - 1 (可用反证法证明,利用上一点)

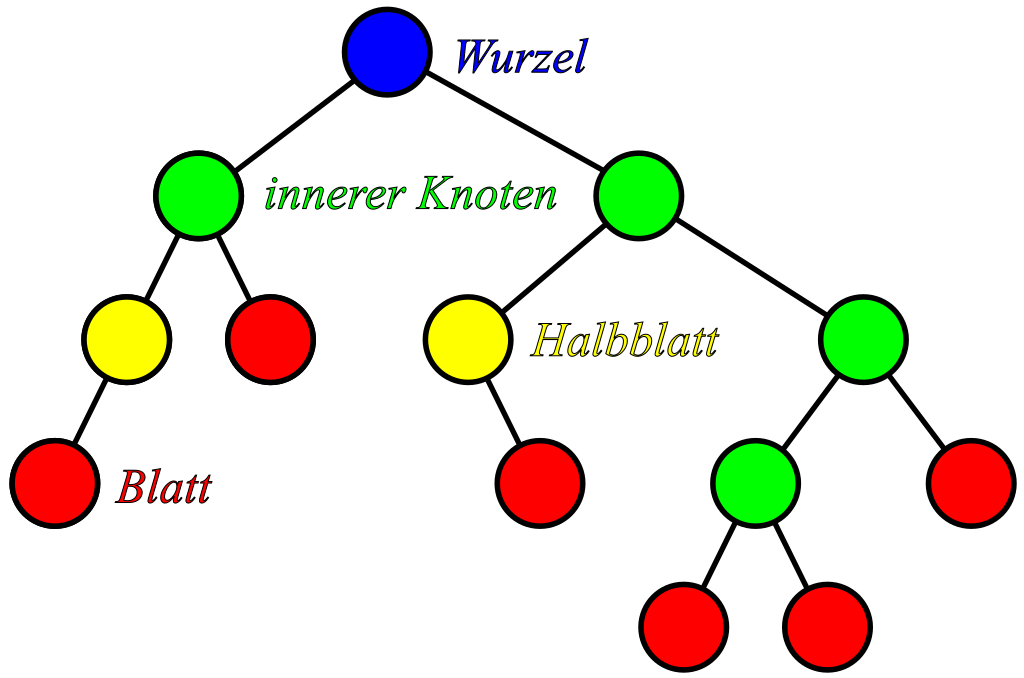
图中红色节点度数为1, 称为叶(Blatt). 图中蓝色为根(wurzel), 黄色为半叶(Halbblatt), 绿色为内部节点(innerer Knoten)

生成树 (Spannbaum [engl. Spanning tree])

设$V=(V_G,E_G)$是一个连通图,一个G的树子图$T = (V_T, E_T)$,当$V_T=V_G\;and\; E_T \subseteq E_G$时,被称为生成树.

简单的说,就是一个覆盖了G的全部顶点,边数最少的图(树)

• 任何一个连通图都存在生成树

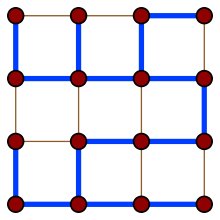
最小生成树 (Minimale Spannbäume [engl. minimum spanning tree])

我们先来看看一张图的权重:就是这张图内所有边的权重之合:

此时我们给图G的边带上权值(通过函数)$m: E \to \mathbb{N}$, $H=(VH,E_H)$是G的子图,那么H的权重为:$w(H):=\sum{e \in E_H} m(e)$

好,让我们设G=(V,E)是一个边带有权重连通图. 当此时G中存在一个权重最小的树T,那么该T就是G的最小生成树:

$W(T) = min(w(T))$

匹配 (Matchings)

一个图是一个匹配（或称独立边集）是指这个图之中，任意两条边都没有公共的顶点。这时每个顶点都至多连出一条边，而每一条边都将一对顶点相匹配。(Wiki)

设G是一个图,那么$M \subseteq E(G)$满足$\forall e_i,e_j \in M$,$e_i,e_j$ 在G中不是相邻关系,则称M是G的一个匹配

完美匹配(perfektes Matching)

简单的说这个点集M包含了G中所有的顶点,叫做完美匹配.

二分图(Bipartite Graphen)

一个无向图G在其顶点集合V可以本拆分成为两个不想交的子集A和B,且边都只连接A和B中的点时,我们称之为二分图.

对于这种非相交的集合A和B的合并,写做$A\biguplus B$,于是一个二分图可以写做$G=(A \biguplus B,E)$

接下来会提到二分图着色,匹配的问题.

定理在这里先提一下,免得找不到:

• 一个图,如果可以二着色,那么它就是二分图.
• 一个图,如果不包含奇数长度环的子图,那么它就是二分图.

二分图的匹配问题

• $G=(V,E), X \subseteq V$
• $\Gamma(X):= \bigcup_{v\in x} \Gamma(v)$被成为X点集的邻域

对于一个二分图$G=(A \biguplus B,E)$,当G存在 $|\Gamma(X)| \ge |X|,for\;all\; X \subseteq A$ 存在$|M|=|A|$

点着色 (Knotenfärbungen von Graphen [engl. ])

一个图的点着色可以看做一个带有k色的图G=(V,E)的函数$c: V\to { 1,\dots ,k }$,有:

$c(u) \neq c(v)$对于所有边${ u,v }\in E$

即对于所有的点上色,使相邻的点颜色不同.

色数 (chromatische Zahl )

一个图的色数常被写做$\chi (G)$,也就是最少需要多少不同的颜色能进行点着色.当 $\chi (G) \leq k$时,我们称为:G k-färbbar我们称为G可以k着色

二分图和着色之间的结论

• 一个图,如果可以二着色,那么它就是二分图.
• 一个图,如果不包含奇数长度环的子图,那么它就是二分图.

有向树(Wurzelbäume [engl. Rooted tree])

(oder auch gerichteter Baum)

不知道中文是不是叫这个

但是看英文名就知道,这种树已经有一个节点被钦点成为根节点.

和无向树不同,无向树任意节点都可以被认为是根.其实还能大概分出Out-Trees和In-Trees这里姑且详细研究了.(貌似没多少教材提,懒)

• 这是一个有向(gerichteter),无循环的(azyklischer)图.
• 其中会有一个点w的入度为0
• 其它节点入度均为1

节点w被成为根节点,出度为0的节点被成为叶节点.

还可以从无向树开始定义,一个有向树为一个二元组(T,w),T是无向树,w作为根.对于T中每一个节点$v\in V$都存在唯一一个Pfad使w到v.(Pfad指顶点不同的通路,详细定义见前面的文章)在让所有Pfad的方向从w指向v.

基本概念

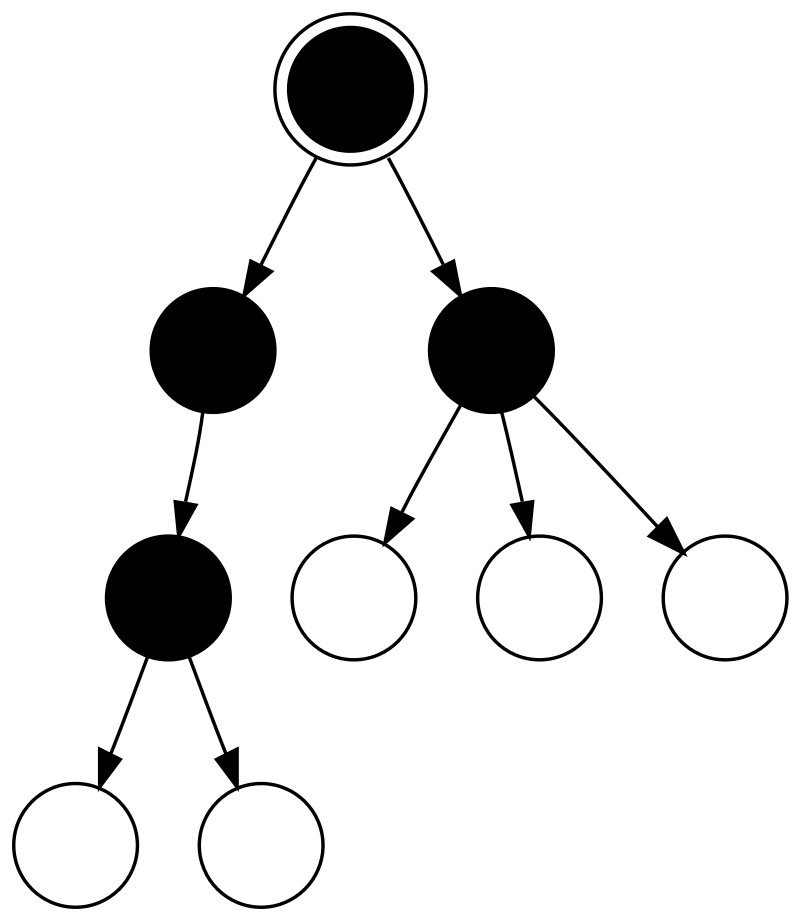
现在把这个树想做一个家族族谱,再想一个非根,非叶节点存在:

• 祖先(Vorgänger)[ascendant]: 在同一条途径上,更接近根节点的那个
• 父节点(Vater): 相邻的祖先节点
• 子嗣,子孙(Nachfolger)[descendant]:在到叶节点同一途径上更接近叶的那个
• 子节点(Kind)[Child]: 相邻子孙节点

树的高度(Höhe von Bäumen)

一棵树的高度是最长的那个从根到叶途径的长度.我严重怀疑这个规矩是德国人定的

高度,层数,深度,不是一个概念,容易乱

某个点的高度是:

1. 那个点所在的,
2. 从根到叶的,
3. 最长的途径,

以叶高度为0,向着根节点递增.

比如”基本概念”下的那张图,右侧有三个子节点的节点,它的高度算1.整个树高为3

深度是倒过来的高度. 层,根就是第一层,往下递增.

二叉树 (Binärbäume)

一个二叉树是一个有根图,每个节点最多只能有两个子节点.

完全二叉树 (vollständiger Binärbaum)

1. 每一个非叶节点必须要有两个子节点
2. 每条途径必须一样长

也就是说在限定高度内,是对称挂满了子节点的

可以归纳证明一个完全二叉树,当其高度为h时存在$2^h$个叶,$2^{h+1}-1$个节点

Termnotation und Baumdarstellung

表达式我们平时使用的是中缀表达式,操作符位于操作数之间

• 前缀表达式(Präfixform)对应先序遍历

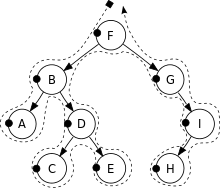
F, B, A, D, C, E, G, I, H.

• 中缀表达式(Infixnotation)对应中序遍历

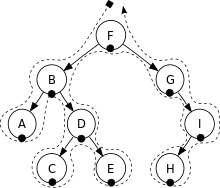
A, B, C, D, E, F, G, H, I.

• 后缀表达式(Postfixform)对应后序遍历

  

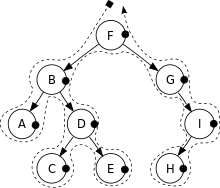
A, C, E, D, B, H, I, G, F.